Как работает катушка индуктивности
Как работает катушка индуктивности
Катушка индуктивности
Что такое катушка индуктивности
Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

В – магнитное поле, Вб
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух – это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссели
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Опыты с катушкой
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Отдалим витки катушки друг от друга
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Что такое катушка индуктивности и для чего она нужна?
Я получил письма от многих из вас с просьбой рассказать простыми словами о катушке индуктивности.
Это действительно хорошая просьба и желание). Потому что катушка индуктивности – это довольно странный компонент. Её невероятно легко сделать. Но немного сложнее понять как она работает.
Катушка индуктивности (иногда называют ее индуктором или дросселем) – это просто катушка проволоки, которая намотана вокруг какого-нибудь сердечника. Ядро сердечника может быть просто воздухом или магнитом.
Когда вы подаете ток через катушку, вокруг неё создается магнитное поле.
При использовании магнитного сердечника магнитное поле будет намного сильнее.
Как работает катушка индуктивности?
Ток через любой провод создаст магнитное поле. Катушка индуктивности имеет проволочную форму, поэтому магнитное поле будет намного сильнее.
Причина, по которой индуктор работает так, как он работает, заключается в этом магнитном поле. Отсюда вытекают и следующие свойства катушки.
Свойства катушки индуктивности:
- Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
- Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
- Катушка индуктивности при протекании тока запасает энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.
Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое (активное) сопротивление, но и реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.
Более детально о принципе работы катушек индуктивности вы можете почитать на сайте.
Для чего вы можете использовать их?
Я почти никогда не использую катушки индуктивности. Главным образом потому, что я работаю в основном с цифровыми схемами. Но я использовал их иногда для создания фильтров, генераторов и блоков питания.
Вы часто найдете катушки индуктивности в аналоговой электронике переменного тока, такой как радиооборудование.
Катушка индуктивности, дроссель.

Катушка индуктивности (inductor. -eng)– устройство, основным компонентом которого является проводник скрученный в кольца или обвивающий сердечник. При прохождении тока, вокруг скрученного проводника (катушки), образуется магнитное поле (она может концентрировать переменное магнитное поле), что и используется в радио- и электро- технике.

К точной и компьютерной технике технике больше близок дроссель (Drossel, регулятор, ограничитель), так как он чаще всего применяется в цепях питания процессоров, видеокарт, материнских плат, блоков питания & etc. В последнее время, применяются индукторы закрытые в корпуса из металлического сплава для уменьшения наводок, излучения, шумов и высокочастотного свиста при работе катушки.


Дроссель служит для уменьшения пульсаций напряжения, сглаживания или фильтрации частотной составляющей тока и устранения переменной составляющей тока. Сопротивление дросселя увеличивается с увеличением частоты, а для постоянного тока сопротивление очень мало. Характеристики дросселя получаются от толщины проводника, количества витков, сопротивления проводника, наличия или отсутствия сердечника и материала, из которого сердечник сделан. Особенно эффективными считаются дроссели с ферритовыми сердечниками (а также из альсифера, карбонильного железа, магнетита) с большой магнитной проницаемостью.

Используется в выпрямителях, сетевых фильтрах, радиотехнике, питающих фазах высокоточной аппаратуры и другой технике требующей стабильного и «правильного» питания. Многослойная катушка может выступать и в качестве простейшего конденсатора, так как имеет собственную ёмкость. Правда, от данного эффекта пытаются больше избавиться, чем его усиливать и он считается паразитным.
Как работает дроссель.
В цепях переменного тока, для ограничения тока нагрузки, очень часто применяют дроссели – индуктивные сопротивления. Перед обычными резисторами здесь у дросселей имеется серьезные преимущества – значительная экономия электроэнергии и отсутствие сильного нагрева.
Каково устройство дросселя, на чем основан принцип его работы?
Устроен дроссель очень просто – это катушка из электрического провода, намотанная на сердечнике из ферромагнитного материала. Приставка ферро, говорит о присутствии железа в его составе (феррум – латинское название железа), в том или ином количестве.
Принцип работы дросселя основан на свойстве, присущем не только катушкам но и вообще, любым проводникам – индуктивности. Это явление легче всего понять, поставив несложный опыт.
Для этого требуется собрать простейшую электрическую цепь, состоящую из низковольтного источника постоянного тока (батарейки), маленькой лампочки накаливания, на соответствующее напряжение и достаточно мощного дросселя (можно взять дроссель от лампы ДРЛ-400 ватт).
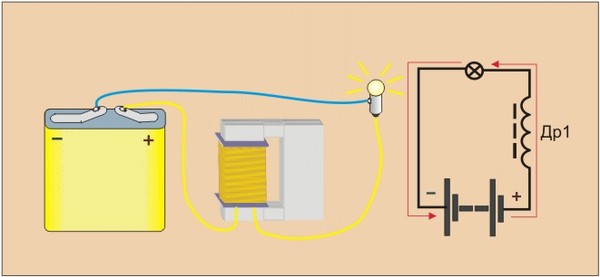
Без дросселя, схема будет работать как обычно – цепь замыкается, лампа загорается. Но если добавить дроссель, подключив его последовательно нагрузке(лампочке), картина несколько изменится.
Присмотревшись, можно заметить, что во первых, лампа загорается не сразу, а с некоторой задержкой, во вторых – при размыкании цепи возникает хорошо заметная искра, прежде не наблюдавшаяся. Так происходит потому что, в момент включения ток в цепи возрастает не сразу – этому препятствует дроссель, некоторое время поглощая электроэнергию и запасая ее в виде электромагнитного поля. Эту способность и называют – индуктивностью.
Чем больше величина индуктивности, тем большее количество энергии может запасти дроссель. Еденица величины индуктивности – 1 Генри В момент разрыва цепи запасеная энергия освобождается, причем напряжение при этом может превысить Э.Д.С. используемого источника в десятки раз, а ток направлен в противоположную сторону. Отсюда заметное искрение в месте разрыва. Это явление называется – Э.Д.С. самоиндукции.
Если установить источник переменного тока вместо постоянного, использовав например, понижающий трансформатор, можно обнаружить что та же лампочка, подключенная через дроссель – не горит вовсе. Дроссель оказывает переменному току гораздо большое сопротивление, нежели постояному. Это происходит из за того, что ток в полупериоде, отстает от напряжения.
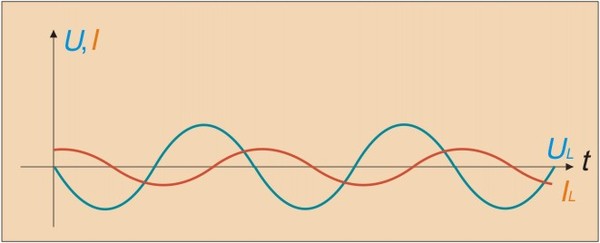
Получается, что действующее напряжение на нагрузке падает во много раз(и ток соответственно), но энергия при этом не теряется – возвращается за счет самоиндукции обратно в цепь. Сопротивление оказываемое индуктивностью переменному току называется – реактивным. Его значение зависит от величины индуктивности и частоты переменного тока. Величина индуктивности в свою очередь, находится в зависимости от количества витков катушки и свойства материала сердечника, называемого – магнитной проницаемостью, а так же его формы.
Магнитная проницаемость – число, показывающее во сколько раз индуктивность катушки больше с сердечником из данного материала, нежели без него(в идеале – в вакууме.)
Т. е – магнитная проницаемость вакуума принята за еденицу.
В радиочастотных катушках малой индуктивности, для точной подстройки применяются сердечники стержеобразной формы. Материалами для них могут являться ферриты с относительно небольшой магнитной проницаемостью, иногда немагнитные материалы с проницаемостью меньше 1.
В электромагнитах реле – сердечники подковоообразной и цилиндрической формы из специальных сталей.
Для намотки дросселей и трансформаторов используют замкнутые сердечники – магнитопроводы Ш – образной и тороидальной формы. Материалом на частотах до 1000 гц служит специальная сталь, выше 1000 гц – различные ферросплавы. Магнитопроводы набираются из отдельных пластин, покрытых лаком.
У катушки, намотанной на сердечник, кроме реактивного(Xl) имеется и активное сопротивление(R). Таким образом, полное сопротивление катушки индуктивности равно сумме активной и реактивной составляющих.
Как работает трансформатор.
Рассмотрим работу дросселя собранного на замкнутом магнитопроводе и подключенного в виде нагрузки, к источнику переменного тока. Число витков и магнитная проницаемость сердечника подобраны таким образом, что его реактивное сопротивление велико, ток протекающий в цепи соответственно – нет.
Ток, переодически изменяя свое направление, будет возбуждать в обмотке катушки (назовем ее катушка номер 1) электромагнитное поле, направление которого будет также переодически меняться – перемагничивая сердечник. Если на этот же сердечник поместить дополнительную катушку(назовем ее – номер 2), то под действием переменного электромагнитного поля сердечника, в ней возникнет наведенная переменная Э.Д.С.
Если количество витков обеих катушек совпадает, то значение наведенной Э.Д.С. очень близко к значению напряжения источника питания, поданного на катушку номер 1. Если уменьшить количество витков катушки номер 2 вдвое, то значение наведенной Э.Д.С. уменьшится вдвое, если количество витков наоборот, увеличить – наведенная Э.Д.С. также, возрастет. Получается, что на каждый виток, приходится какая-то определенная часть напряжения.
Обмотку катушки на которую подается напряжение питания (номер 1) называют первичной. а обмотка, с которой трансформированое напряжение снимается – вторичной .
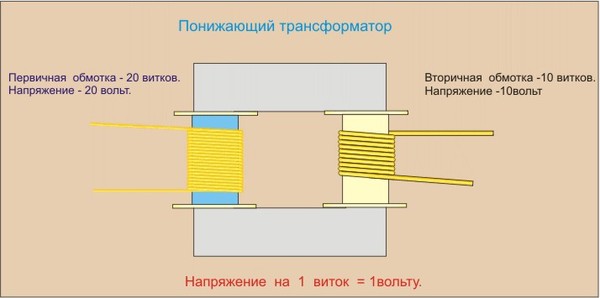
Отношение числа витков вторичной(Np ) и первичной (Ns ) обмоток равно отношению соответствующих им напряжений – Up (напряжение первичной обмотки) и Us (напряжение вторичной обмотки).
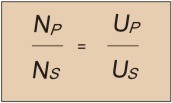
Таким образом, устройство состоящее из замкнутого магнитопровода и двух обмоток в цепи переменного тока можно использовать для изменения питающего напряжения – трансформации. Соответственно, оно так и называется – трансформатор .
Если подключить к вторичной обмотке какую-либо нагрузку, в ней возникнет ток(Is ). Это вызовет пропорциональное увеличение тока(Ip ) и в первичной обмотке. Будет верным соотношение:
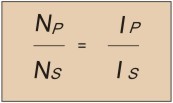
Трансформаторы могут применяться как для преобразовния питающего напряжения, так и для развязки и согласования усилительных каскадов. При работе с трансформаторами необходимо обратить внимание на ряд важных параметров, таких как:
1. Допустимые токи и напряжения для первичной и вторичной обмоток.
2. Максимальную мощность трансформатора – мощность которая может длительное время передаваться через него, не вызывая перегрева обмоток.
3. Диапазон рабочих частот трансформатора.
Параллельный колебательный контур.
Если соединить катушку индуктивности и конденсатор – получится очень интересный элемент радиотехники – колебательный контур. Если зарядить конденсатор или навести в катушке Э.Д.С. используя электромагнитное поле – в контуре начнут происходить следующие процессы: Конденсатор разряжаясь, возбуждает электромагнитное поле в катушке индуктивности. Когда заряд истощается, катушка индуктивности возвращает запасенную энергию обратно в конденсатор, но уже с противоположным знаком, за счет Э.Д.С. самоиндукции. Это будет повторяться снова и снова – в контуре возникнут электромагнитные колебания синусоидальной формы. Частота этих колебаний называется резонансной частотой контура, и зависит от величин емкости конденсатора(С), и индуктивности катушки (L).

Параллельный колебательный контур обладает очень большим сопротивлением на своей резонансной частоте. Это позволяет использовать его для частотной селекции(выделения) в входных цепях радиоаппаратуры и усилителях промежуточной частоты, а так же – в различных схемах задающих генераторов.
Цветовая и кодовая маркировка индуктивностей.
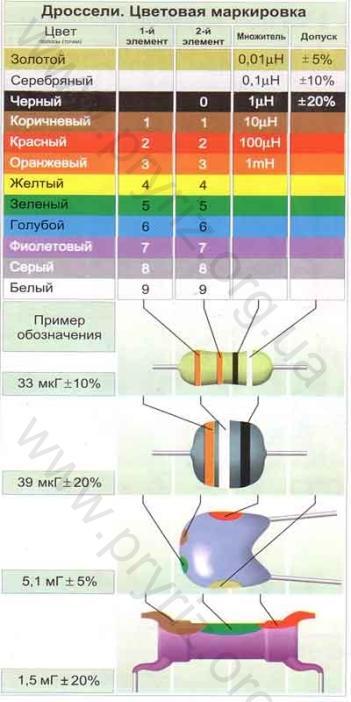
Обычно для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Номинальное значение кодируется цифрами, а допуск — буквами. Применяется два вида кодирования.
Первые две цифры указывают значение в микрогенри (мкГн), последняя — количество нулей. Следующая за цифрами буква указывает на допуск. Например, код 101J обозначает 100 мкГн ±5%. Если последняя буква не указывается —допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.
D=±0,3 нГн; J=±5%; К=±10%; M=±20%


Индуктивности маркируются непосредственно в микрогенри (мкГн). В таких случаях маркировка 680К будет означать не 68 мкГн ±10%, как в случае А, а 680 мкГн ±10%.

Как измерить индуктивность катушки, дросселя.
ЗЫ: Взял где взял, обобщил и добавил немного.
Простите за качество некоторых картинок (чем богаты).
Берегите себя и своих близких!

Как измерить индуктивность катушки мультиметром? Взять мультиметр с функцией измерения индуктивности. Лодку мне.
И много мультиметров измеряет индуктивность? И сколько они стоят?
99 из ста, что у вашего прибора нет такой функции.
причём, мультиметр имеет минимальный предел 2мГн. например, дроссель с матплаты им измерить нельзя.
ОП, правильно писать “котушка”. Ударение на О.
Как работает катушка индуктивности
Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
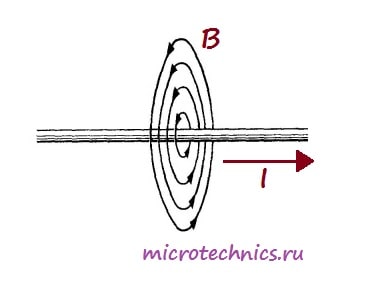
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
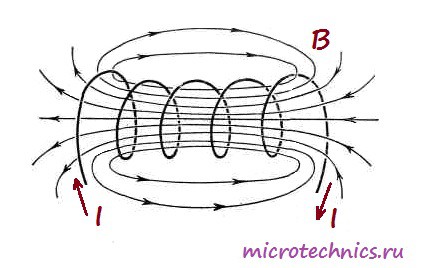
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
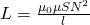
Давайте разберемся, что за величину входят в это выражение:
 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению:
– магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: 
 – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.
– магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз. – площадь поперечного сечения катушки
– площадь поперечного сечения катушки – количество витков
– количество витков – длина катушки
– длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь.
Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
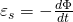
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку 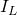 будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
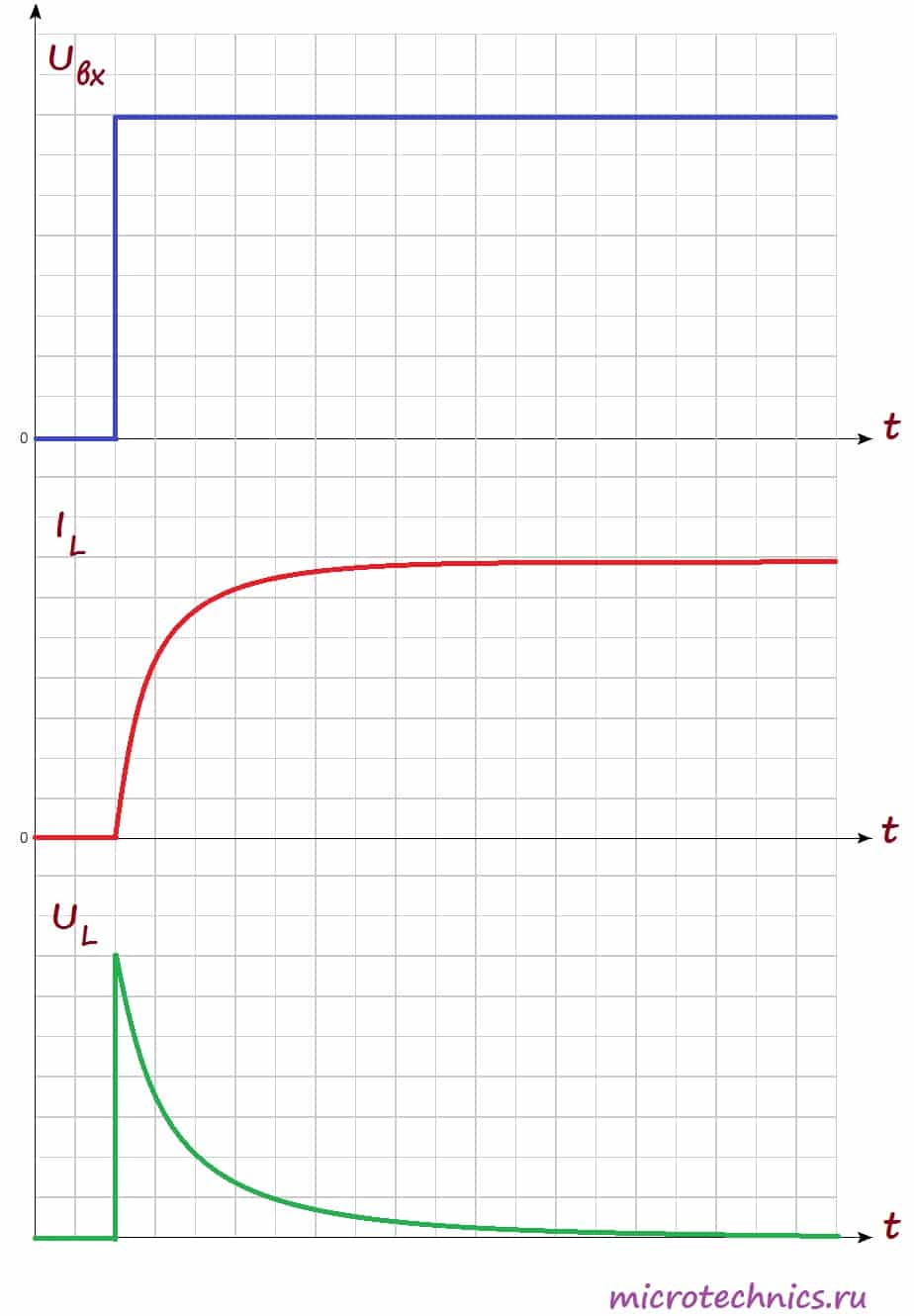
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
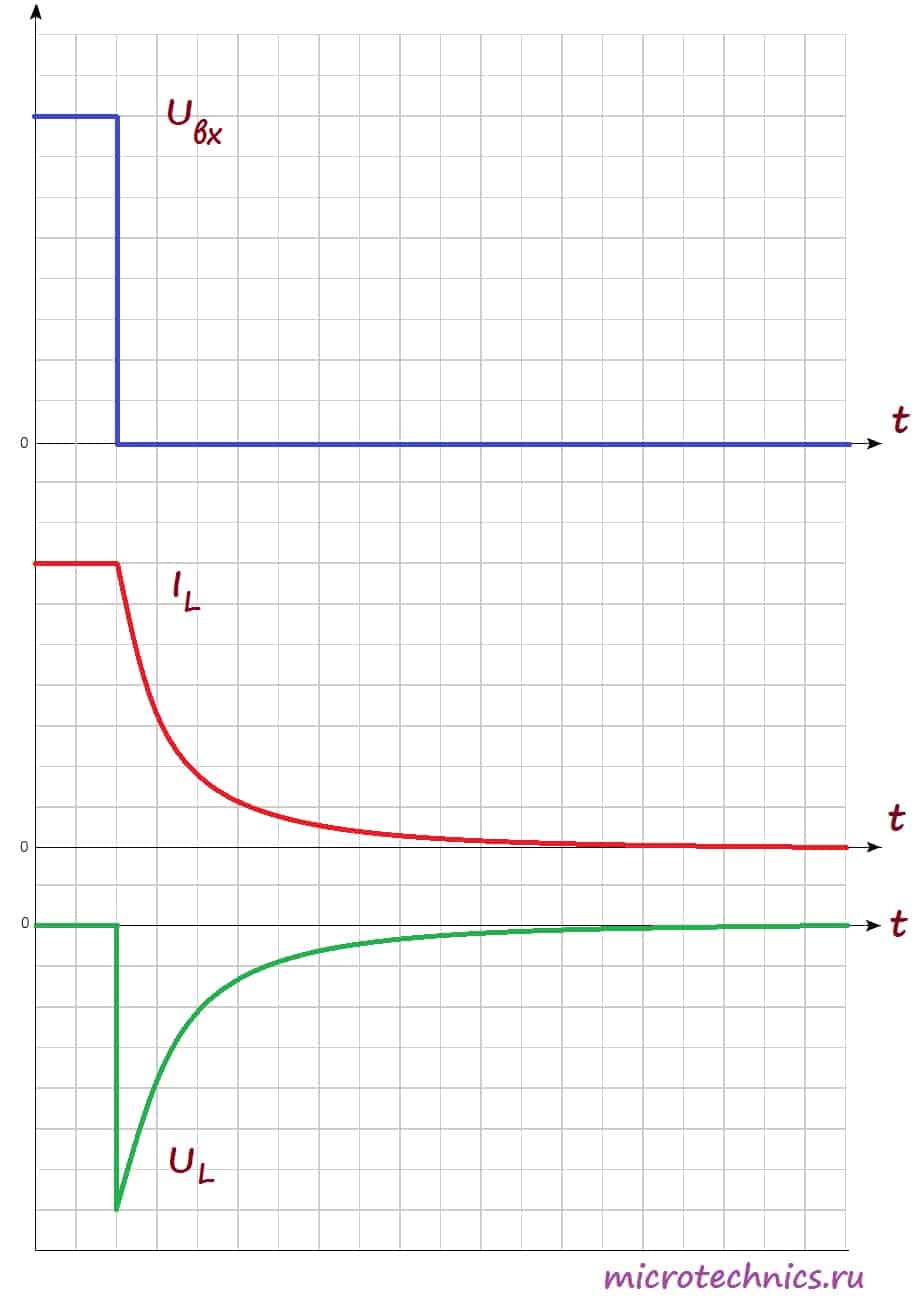
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
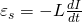
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
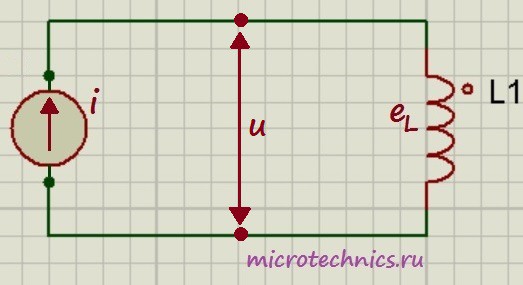
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
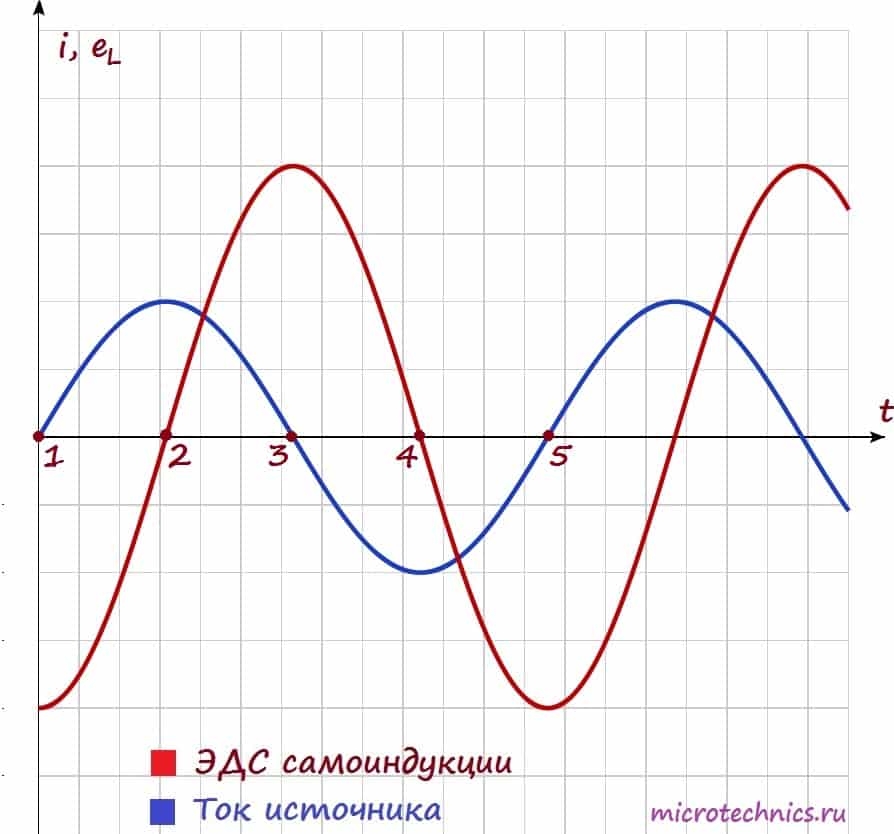
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
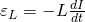
Собственно, график нам и демонстрирует эту зависимость Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2:  ,
, 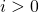 0″ title=”Rendered by QuickLaTeX.com” height=”12″ width=”39″ style=”vertical-align: 0px;”/>, участок 3-4:
0″ title=”Rendered by QuickLaTeX.com” height=”12″ width=”39″ style=”vertical-align: 0px;”/>, участок 3-4: 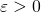 0″ title=”Rendered by QuickLaTeX.com” height=”12″ width=”41″ style=”vertical-align: 0px;”/>,
0″ title=”Rendered by QuickLaTeX.com” height=”12″ width=”41″ style=”vertical-align: 0px;”/>,  ). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника). А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока). И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника). А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока). И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
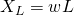
Где 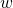 – круговая частота:
– круговая частота: 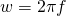 .
. 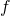 – это частота переменного тока.
– это частота переменного тока.
Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный ( 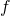 = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
= 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение 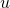 ? Здесь все на самом деле просто По 2-му закону Кирхгофа:
? Здесь все на самом деле просто По 2-му закону Кирхгофа:
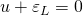
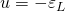
Построим на одном графике зависимости тока и напряжения в цепи от времени:
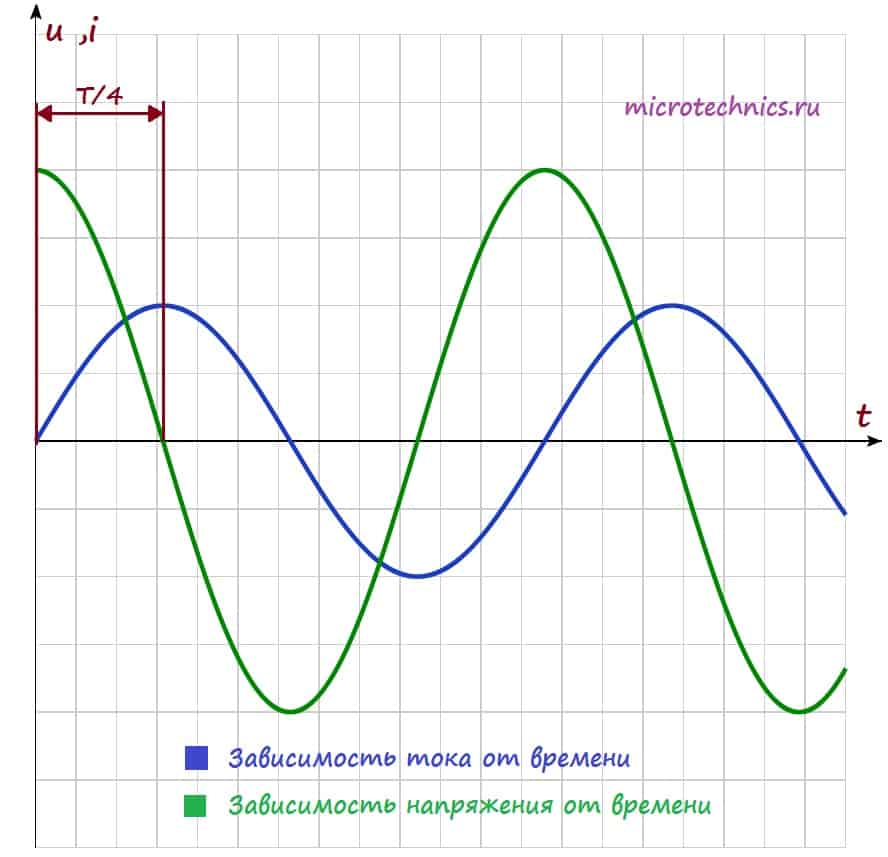
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому дальнейший разговор о катушках индуктивности мы будем вести в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Что такое катушка индуктивности и почему ее иногда называют дроссель
Катушка индуктивности характеризуется своими параметрами, главными из которых являются ее индуктивность, сопротивление обмоток и рабочий ток, с которым она может функционировать. При составлении схемы особую важность играют ее габариты, вес. К катушкам предъявляются особые требования, которые могут различными в зависимости от сферы ее применения. Для использования в преобразователях, фильтрах, катушки используются более мощные, чем это заложено схемой. Главное выбрать такую модель, которая не будет влиять на производительность всей схемы или цепи.
В статье будет рассказано о том, что это такое, где используется такая катушка безопасности и из чего состоит. Также в статье содержится видеоролик и дополнительный материал, который поможет лучше разобраться в выбранной теме.

Обзор пассивных компонентов
Современная радиоэлектронная аппаратура (РЭА) содержит огромное количество электрорадиокомпонентов, т.е. самостоятельных изделий, выполняющих определенные функции. Электрорадиоэлементы подразделяют на активные и пассивные. К активным относятся транзисторы, микросхемы ,электронные лампы и т.д., т. е. элементы, способные усиливать или преобразовывать электрические сигналы. К пассивным относятся резисторы, катушки индуктивности, конденсаторы, трансформаторы, коммутационные элементы, т. е. такие элементы, которые предназначены для перераспределения электрической энергии.

Пассивные компоненты по сути соответствует пассивному элементу схемы. Пассивные компоненты характеризуются малыми размерами, малым числом выводов (как правило, два-три), низкой стоимостью и, как правило, достаточно высокой стойкостью к воздействиям при сборке узлов. Пассивные элементы могут выступать как дискретные компоненты и как элементы интегральных микросхем. В РЭА интегральные микросхемы имеют очень большой удельный вес, но пассивные компоненты являются все же самыми распространенными изделиями электронной промышленности. Это можно объяснить тем, что некоторые элементы трудно выполнить в микросхемном исполнении. Практически невозможно в ИМС изготовить конденсаторы большой емкости, резисторы с большим сопротивлением, сложности в разработке интегральных катушек индуктивности и трансформаторов. Кроме того технические характеристики дискретных элементов лучше, чем интегральных.
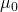 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению:
– магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: 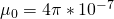
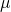 – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.
– магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз.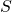 – площадь поперечного сечения катушки
– площадь поперечного сечения катушки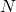 – количество витков
– количество витков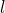 – длина катушки
– длина катушки